|
The Mystery of the Land of Riemannia
|
|
Somewhere, far behind one of the infinite dimensions of Hilbert space, there is the Land of Riemannia. It was discovered in 1859 by Bernhard Riemann (1826-1866), and so it bears his name. Riemann was a mathematician, and also the few pioneers who entered this land were mathematicians. This might frighten some of you, but let me nonetheless some tell me remarkable facts about it.
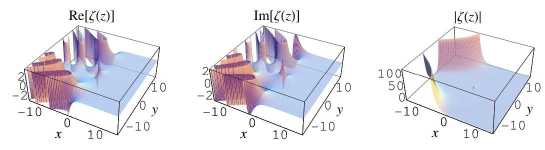
Certainly, one of the most astonishing things about this land is that you can shoot two distinct photographs of the same lanscape: the landscape is four-dimensional!
The mathematicians call the “landscape” the
graph of the Riemann Zeta function,
in symbols ![]() , where s is a so-called complex
number. Complex numbers contain the square roots of negative numbers,
especially the number
, where s is a so-called complex
number. Complex numbers contain the square roots of negative numbers,
especially the number
![]() . They can be represented as points
of a plane, one of whose both spanning axes is formed by the real numbers.
This “real axis” is the “East-West direction” of our landscape,
the South-North direction being spanned by the “imaginary axis”.
The zeta function itself also takes complex values, and therefore
its graph is four-dimensional.
. They can be represented as points
of a plane, one of whose both spanning axes is formed by the real numbers.
This “real axis” is the “East-West direction” of our landscape,
the South-North direction being spanned by the “imaginary axis”.
The zeta function itself also takes complex values, and therefore
its graph is four-dimensional.
On a photograph, however, we can only project three dimensions, so the mathematicians use a trick to represent the graph (remember: the “landscape”) in two different parts, the “real part” and the “imaginary part”. To combine these two different perspectives of the same landscape, some mathematicians also observe the “absolute value”, that is the distance of a point of the landscape from the origin of the complex plane. Some of you probably will recognize this as the length of the corresponding vector, and its square is given by the sum of the squares of the real and the imaginary part, according to the theorem of Pythagoras. The photograph of the absolute value therefore gives a slightly distorted, but nevertheless important, view on the landscape of Riemannia.
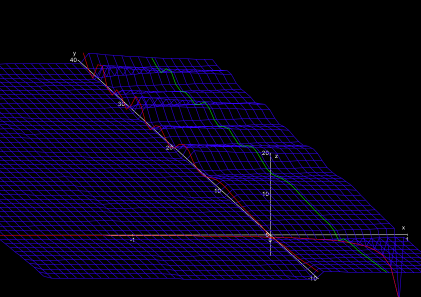
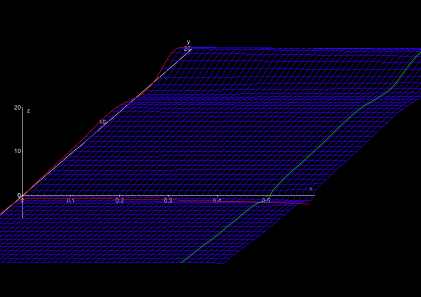
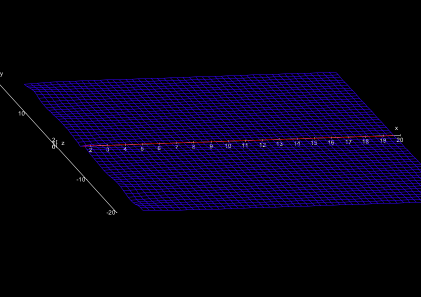
Putting on the “real glasses”, you see the part “Real-Riemannia”. This is a weird countryside. In the East, there extends a wide, slightly descending plain (Fig. 2). To the West, you slowly rising ridges, being oriented exactly in East-West direction.
|
|
|
|
|
|
|
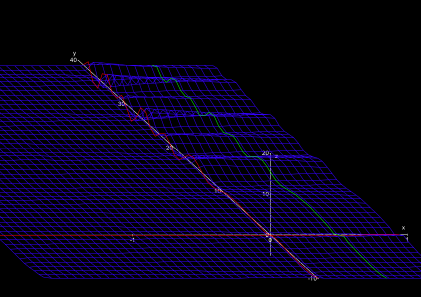
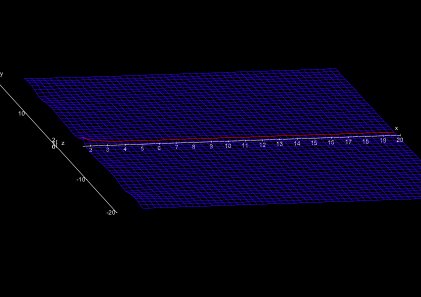
At a special site (at the coordinate s = 1) we find an infinitely high steep mountain, being directly neighbored by an infinitely deep abyss. This site should be avoided advisably. However, Riemann already noticed that this is the only dangerous (“singular”, as the mathematicians call it) location in the whole land. (Fig. 3). In the “real perspective”', the abyss is in the West of the mountain, in the “imaginary perspective” it is in the North of it.
|
|
|
|

|
|
|
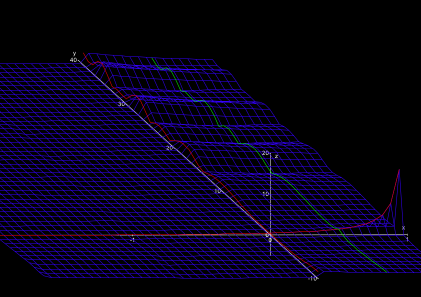
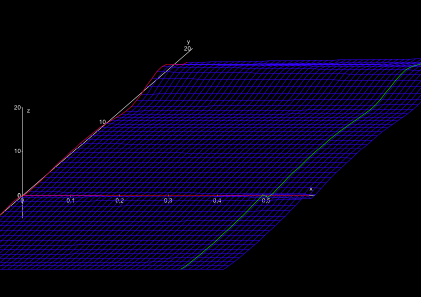
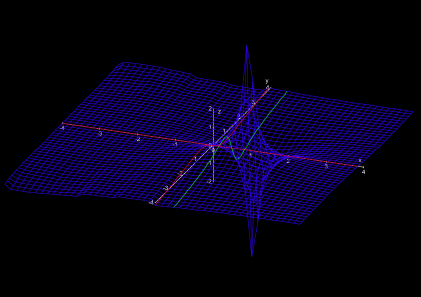
At the zeroth degree of longitude in South-North direction (the imaginary axis s = iy), the character of the landscape suddenly changes. The gentle ridges abruptly abandon and pass into very calm, gently wavy plain (Fig. 4).
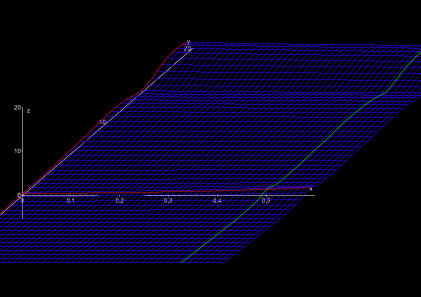
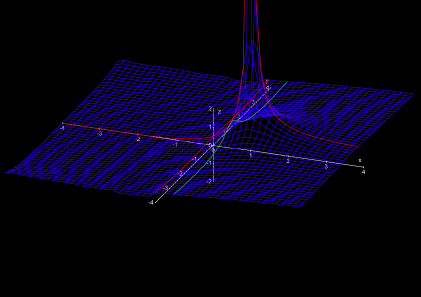
However, the peaceful impression of the new landscape deceives. In the Northwest and the Southwest there pile up giant mountains with steep peaks and cliffy abysses (Fig. 5). Contrary to the singularity s = 1, however, the mountains and abysses have finite height or depth, they are no singularities. They fringe a narrow shrinking valley around the zeroth degree of latitude (the “real axis” Im s = 0).
|
|
|
|

|

|
|
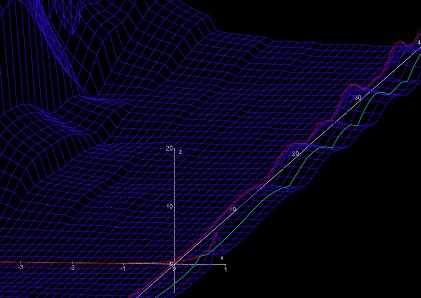
The greatest mystery of the land of Riemannia is the distribution of the “zeros”. For the mathematicians, these are those locations, which are at sea level both in the real part and the imaginary part. By far the most points of Riemannia are not at sea level. For instance, the whole plain East of the singularity s = 1 is above sea level, and even the cliffy mountains in the west are never at sea level for real and imaginary part simultaneously.
Only on two straight lines such zeros are known, on the real axis
and on the “critical line”.
On the real axis Im s = 0, i.e., the zeroth degree of latitude
in the West, exactly the negative even values of s are zeros,
s = -2, -4, -6, ...
These are the so-called “trivial zeros”.
The critical line, on the other hand, is parallel to the imaginary
axis (a “longitude” in South-North direction), namely all numbers
with real part ![]() , i.e.,
, i.e.,
![]() .
In the figures, the critical line is sketched in green.
.
In the figures, the critical line is sketched in green.
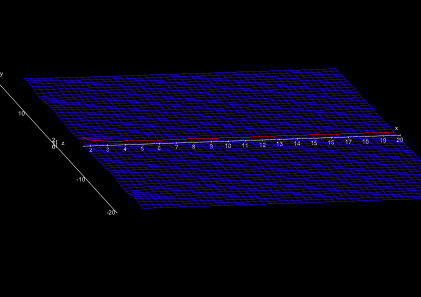
The only thing which is known to date is that the nontrivial zeros are on the “critical strip” between the degrees 0 and 1 of longitude, i.e., 0 < Re s < 1 (Fig. 6), that there are infinitely many zeros on the critical line, and that at least 40% of all nontrivial zeros are on the critical line.
But no-one knows to date whether in fact all nontrivial zeros lie on the critical line. That this is the case is the Riemann Hypothesis. This mystery is so important for the mathematicians that the one who strictly proves that all nontrivial zeros of the zeta function lie on the critical line will receive a reward of $1 Million! Interestingly, there seems to be no reward if the hypothesis was wrong and someone finds at least one counter-example: in this case, the Riemann hypothesis problem could perhaps be solved, but there was no prize ....
If you want to explore the land of Riemannia on your own, you can start an animation which shows its landscape (at least for comparably small values of s) with the small Java program which :
http://math-it.org/Mathematik/Riemann/riemann.jar
(It requires Java JRE 6 or higher).
You can adjust the ranges of the plotted values Re s, Re s, and z, where s = Re s + i Im s, and z = Re ζ(s), z = Im ζ(s), or z = |ζ(s)|, respectively.
In the plot, the real and imaginary lines are projected on the graph and are marked red. The so-called "critical line" (Re s = 1/2) is marked green; the famous Riemann hypothesis conjectures that all zeros besides s = -2, -4, -6, .... lie on the critical line.
If your browser has installed Java Applets, you can quickly start the program by simply clicking the button:
- Marcus du Sautoy: The Music of the Primes. Why an Unsolved Problem in Mathematics Matters. Fourth Estate, London 2003
- http://www.maths.tcd.ie/pub/HistMath/People/Riemann/ – Biography and original papers of Bernhard Riemann
- http://www.claymath.org/millennium-problems/riemann-hypothesis – The Riemann hypothesis as one of the Millenium Problems of Clay Mathematics Institute, for the solution of which there is a prize of $1 million.
| © de Vries 2004–2015 |
|
|